Hoekom doen ons wiskunde agterstevoor?
François Durand
Het jy al agtergekom dat ons eintlik wiskunde agteruit doen? Doen maar enige optel, aftrek, maal of deel som, veral as jy groterige getalle het, en kyk in watter rigting doen jy dit en hoe skryf jy die antwoord neer – van regs na links!
Dit is veral opvallend dat die rigting waarin ons tel en die rigting waarin ons lees verskil. Probeer byvoorbeeld vinnig die volgende getal te sê: 98405203119. As Westerling wat aandring daarop om van links na regs te lees moet jy daardie getal eers in drieë opbreek om die honderde, duisende en miljoene te identifiseer voor jy dit kan lees – en let mooi op wat jy doen: jy begin dit van regs na links in drieë op te breek voor jy dit van links na regs lees.
Weet jy hoe doen ‘n Arabier dit? Hy lees eenvoudig die getal van regs na links sonder om enige opbrekery te doen. As ons wou, sou ons alles kon omdraai en dit anderkant om doen – met ander woorde 1234 sal dan een-en-twintig driehonderd vierduisend gewees het en nie eenduisend tweehonderd vier-en-dertig nie. So hoekom doen ons nie wiskunde van links na regs nie?
Maar eers wil ek jou aan ‘n man met die naam Leonardo van Pisa, of Fibonacci soos mense hom leer ken het, voorstel.

Fibonacci is veral ook bekend vir sy Fibonacci-getalle wat uit ‘n reeks getalle bestaan waarvan elke getal uit die som van die twee voorafgaande getalle bestaan, naamlik: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
Met ander woorde: 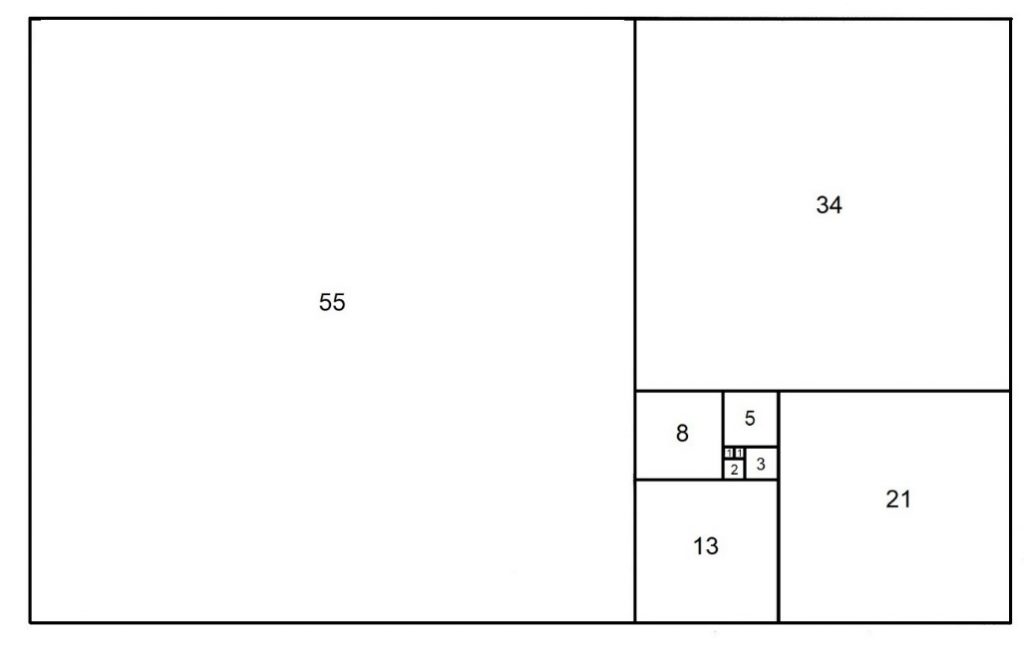
0+1=1
1+1=2
1+2=3
2+3=5
3+5=8
5+8=13
8+13=21
13+21=34
21+34=55
34+55=89
ensovoorts.
Dit klink soos sommer lawwe sommetjies, maar dit is eintlik die wiskundige formule vir ‘n tipe spiraal – en iets wat mens soms in die natuur raakloop (of ten minstens naasgenoeg, want die spirale in die natuur is nie altyd presies vergelykbaar met die Fibonacci-getalle nie).
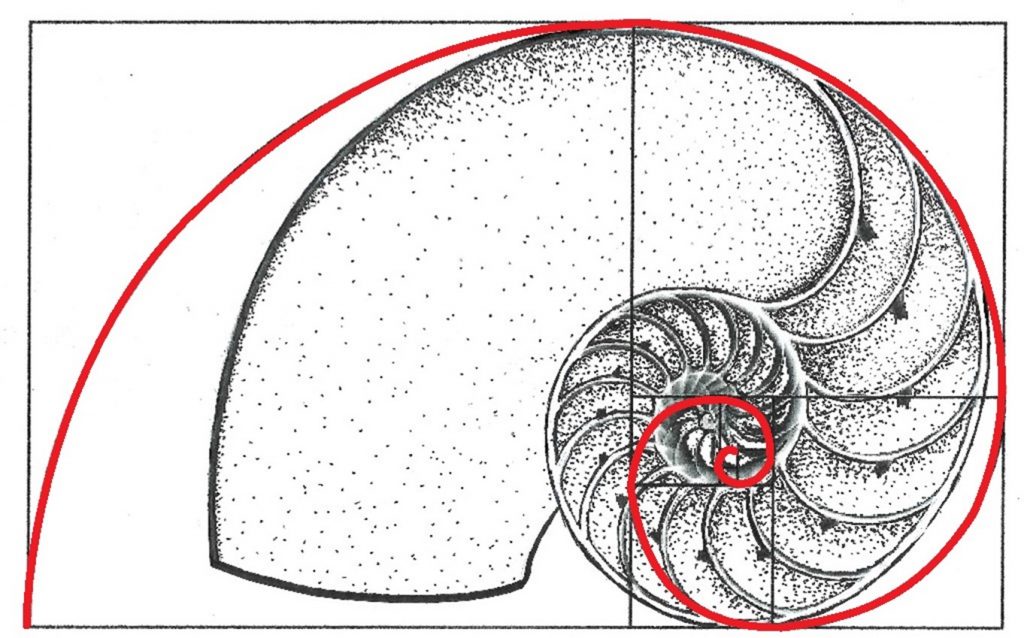
‘n Voorbeeld van hoe die Fibonacci getalle nie met ‘n spiraal in die natuur ooreenstem nie. Mens se verbeelding hol soms met mens weg, veral as mens romantiese, idilliese of metafisiese sienings oor goed het.
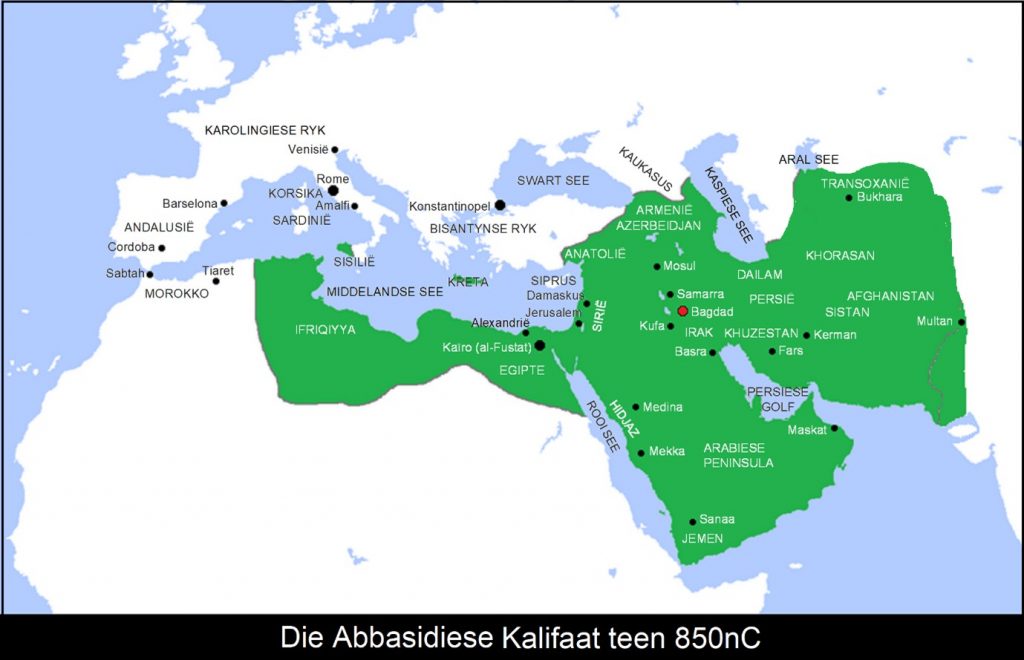
Maar tog het ons Leonardo van Pisa se entoesiasme nodig om die res van die storie te vertel. Toe hy ‘n jong man was, het hy saam met sy pa, ‘n handelaar en doeanebeampte, in die 12de eeu in die Maghreb gewerk. Die Maghreb is ‘n baie belangrike deel van die storie en dus het ek hierdie kaart ingesluit.
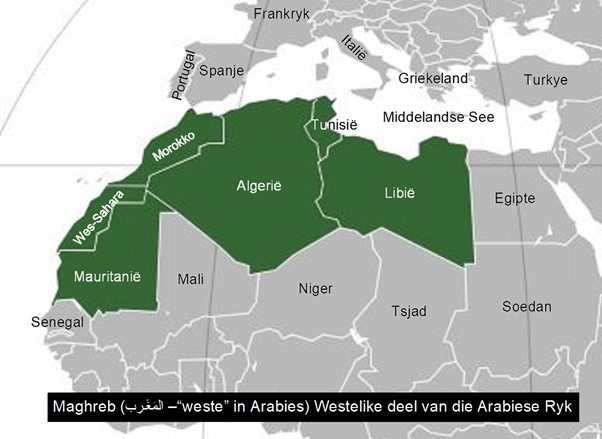
Die politieke grense van die lande het natuurlik nie in daardie tyd bestaan nie en was eers eeue later deur Europese lande, wat Noord Afrika tussen hulle opgedeel het, aangebring. Die oostelike deel van die Arabiese Ryk word terloops die Mashrek genoem as jy wonder, maar omdat dit nie deel van hierdie storie is nie gaan ek nie ‘n kaart daarvan insluit nie.
In die Maghreb het die Van Pisas met Berber-handelare en boekhouers te doen gekry. Die Berbers het die Hindoe-Arabiese getallestelsel gebruik wat Leonardo gefassineer het. Hy was oorstelp van verwondering oor die logika en praktiese uitvoerbaarheid van hierdie getallestelsel want, soos hy in sy boek Liber Abaci (Die boek van die abakus) in 1202 geskryf het: met hierdie tien Arabiese syfers, kan mens enige getal uitskryf!
Leonardo se entoesiasme klink simpel omdat ons so gewoond is aan die Arabiese getallestelsel dat ons onself beswaarlik kan indink dat daar enige alternatief kan wees.
In daardie tyd was die Romeinse getallestelsel nog steeds meestal in Europa gebruik, alhoewel die Arabiere, wat in Andalusië op die Iberiese Peninsula (Spanje van vandag) gebly het, hulle eie getallestelsel en wiskunde gehad het.
Die probleem met die Romeinse getallestelsel is dat dit uit ‘n redelike arbitêre bondeling van simbole bestaan het, bv. VI is 6, VII is 7, VIII is 8, XI is 11 en XII is 12, maar daar is nie getalle soos IIIV of IIV of IIIX of IIX nie. Vandag is meeste mense vertroud met die Romeinse I wat 1 simboliseer, II is 2, III is 3, V is 5, X is 10, L is 50, C is honderd, D is vyfhonderd en M is duisend, maar daar is nie ‘n simbool vir 5000 nie en dus stop hulle getalle by MMMCMXCIX (3999) want hulle kon nie 4000 as 1000 minder as 5000 uitdruk nie. Onthou dat IV (4) is een minder as V (5), en XL (40) is 10 minder as L (50), en CD (400) is 100 minder as D (500) in die Romeinse getallestelsel.
Dit is veral ‘n dilemma as mens in ag neem dat hulle legioene soldate gehad het en iemand moes verantwoordelikheid vir die uitbetaling van hulle salarisse gewees het. ‘n Legioen het tussen 5000 en 6000 soldate gehad. Die Romeine het ‘n slim manier ontdek om groot getalle uit te druk deur om eenvoudig ‘n strepie bokant ‘n getal te sit wat gesimboliseer het dat daardie getal met ‘n duisend vermenigvuldig moet word. Met ander woorde V̄Ī is 6000, en M̄ is een miljoen. Mens sou natuurlik wel miljoene of duisendstes van getalle by 3999 kon las, maar dit was slordig en lomp.
Die lompheid van die sisteem kan geïllustreer word deur die getal 999 wat in Romeins as: CMXCIX uitgedruk word en nie as IM nie. Groot getalle was elkeen ‘n oefening in optel en aftreksomme bv. CMXCIX is 1000-100+100-10+10-1. Enige skoolkind kan mos uitwerk dat -100+100-10+10 nul is en dat die boonste getal eintlik as 1M of 1000-1 uitgedruk kon word, buiten vir die feit dat Romeine nie nul gehad het nie en dus nie die sommetjie kon doen nie!
Buiten vir die feit dat die Romeine nie ‘n simbool (of die konsep van) nul gehad het nie (wat ook die rede is dat ulle nie ‘n jaar 0 gehad het nie), was die Romeinse sisteem vererger deurdat hulle ook nie negatiewe getalle – met ander woorde heelgetalle kleiner as 1 gehad het nie, en buiten die konsep van halwes, derdes, kwarte, driekwarte, sesdes en twaalfdes, het hulle nie desimale getalle gehad nie. Met ander woorde dit was vir hulle baie moeilik om deelsomme te doen.
Probeer bietjie 1674 met 48 deel deur om slegs Romeinse syfers te gebruik – met ander woorde deel MDCLXXIV deur XLVIII en dan sal jy Leonardo van Pisa se entoesiasme met die Arabiese stelsel deel.
Die geheim van die Hindoe-Arabiese getallestelsel is dat dit ‘n posisionele sisteem is. Dit bedoel dat die ene die eerste posisie van die posisionele sisteem inneem, tiene die tweede posisie, honderde die derde posisie, duisendes die vierde posisie ensovoorts. Hierdie sisteem kan met enige grondtal gebruik word, maar toevallig het die Hindoe-Arabiese stelsel, nes die Romeinse stelsel, die grondtal 10 gebruik (meer oor grondtalle later).
Die ry Arabiese getalle begin inderwaarheid met 0 en dus moet dit so lees:

Wanneer mens by 10 kom, en omdat ons getallestelsel op die grondtal 10 gegrond is, spring die volgende getal (10) na die volgende plek in die positionele sisteem: met ander woorde 10 waar 0 die plekhouer is en die 1 op die tweede posisie van regs ‘n volle stel getalle in die eerste vlak van die grondtal 10 plus een verteenwoordig.
So kan mens aanhou tel totdat die getal 99 bereik word waarna die volgende getal 100 na die derde plek van regs, naamlik die honderde spring en die twee nulle wat dit voorafgaan (let op nie daarna geskryf word nie aangesien dit van regs na links gelees moet word) plekhouers is. Daar was ook geen noodsaak om nuwe simbole te skep vir al hoe groter getalle, soos die Romeine moes doen nie.
Toe die Arabiese Ryk tot by Indië gestrek het, het hulle ontdek dat die Hindoes onfhanklik ‘n baie gesofistikeerde wiskunde ontwikkel het. Hierdie wiskundige stelsel, wat die syfer 0 en getalle soortgelyk aan dié wat ons vandag gebruik, was in die Arabiese wiskunde opgeneem. Die woord syfer (“sifr” in Arabies) is die naam vir nul.
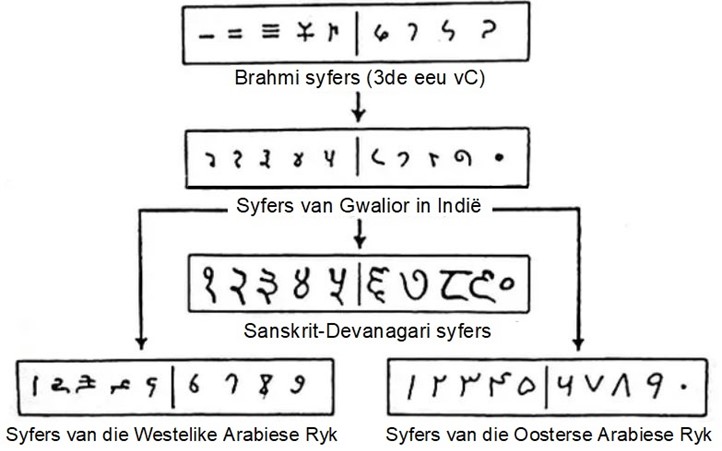
Leonardo van Pisa het hierdie nuwe getallestelsel in sy boek Liber Abaci (die boek van die abakus) opgeskryf en op hierdie manier in Europa gepolulariseer.

Leonardo van Pisa was egter nie die eerste Europeër wat iets oor die Arabiese getalle te sê gehad het nie – die Codex Vigilanus of Codex Albeidensis van 976nC, wat die geskiedenis van die Iberiese Peninsula (hedendaagse Spanje) gedek het, het ook melding gemaak van die getallestelsel van die Arabiere in al-Andalus of Andalusië.
Leonardo van Pisa, wat ‘n wiskundige was, kon egter die belangrikheid van die Arabiese getallestelsel insien en het dit in gebruik geneem. Met die koms van die drukpers in die 15de eeu het die gebruik van die Arabiese getalle en telwyse wyd deur Europa versprei en van daar, na die res van die wêreld. En dis die rede hoekom jy vandag nog steeds, meer as agt eeue later, dit gebruik.
Maar dis nie die hele storie nie. Een van die nuttigste vorms van wiskunde is algebra. Sonder algebra is dit onmoontlik om fisika, chemie, sterrekunde, biologie of geologie of enige ander wetenskap te doen. Die Berbers was deel van ‘n eeue oue tradisie wat tydens die Goue Era van die Arabiese Ryk (7de-13de eeu nC) ontwikkel was. Bagdad was die middelpunt van hierdie ryk en het dieselfde rol as Alexandria van ouds gespeel.
Geleerdes het van heinde en ver na Bagdad gereis om daar in die geselskap van ander geleerdes gedagtes uit te ruil. Die Huis van Wysheid of Die Groot Biblioteek van Bagdad was die plek waar skrywers, vertalers, filosowe, wiskundiges en wetenskaplikes daagliks bymekaar gekom het. Dit was, soos die Biblioteek van Alexandrië en die Aristoteles se Lycaeum in Athene, ‘n plek van akademie – so na as wat mens aan ‘n universiteit in daardie tyd kon kry.
Die Huis van Wysheid het honderdduisende geskrifte gehuisves, onder andere die werke van die Griekse filosowe wat in Middeleeuse Europa verbrand is. Hier, soos in die biblioteke van Damaskus en Kaïro, was geskrifte in Siries, Persies en Grieks na Arabies vertaal. Boeke van papier was gemaak danksy die Chinese wat die Arabiere die kuns van papiermaak geleer het. Van die staanspoor het die Arabiere hierdie biblioteke as die bergplekke van die kennis van die hele wêreld beskou – ten bate van almal en nie slegs Arabiere nie. Vanuit hierdie samekoms van geleerdes was vakke soos filosofie, wiskunde, astronomie, fisika, chemie, ingenieurswese, biologie en medies gevestig. Groot deurbrake en vordering was in hierdie vakke oor die volgende vier eeue gemaak. Dit is dan ook nie verbasend dat ongeveer twee derdes van benoemde sterre Arabiese name het nie.
Muhammad ibn Musa al-Khwarizmi, ‘n astronoom en wiskundige, was in 820 nC as die hoof van die Huis van Wysheid aangestel. Hy het ‘n boek getiteld: Kitab al-Jabr geskryf waar hy algoritmes verduidelik. Al-jbr wat “samevoeging van dele” in Arabies beteken, is die oorsprong van die woord algebra. Al-Khwarizmi word as die Vader van Algebra beskou want hy het hierdie tipe wiskunde gepopulariseer.

En dit is die rede hoekom ons Arabiese syfers, die posisionele getallestelsel en algebra gebruik en van regs na links wiskunde doen – want die Arabiere het dit vir ons geleer.
Nadat die Mongoolse barbare die Huis van Wysheid tydens die Beleg van Bagdad in 1258 afgebrand het, en Bagdad geval het, het dit ook die einde van die Goue Era van die Arabiese Ryk ingelui. Tydens die Renaissance wat ‘n eeu en ‘n half daarna in Italië begin het, was van die Arabiese geskrifte wat gered kon word, weer in Latyn vertaal en so was ‘n groot deel van Europa se verlore filosowe, wiskundiges en wetenskaplikes se werk teruggekry saam met ‘n stortvloed inligting wat deur die Arabiere in die voorafgaande eeue versamel is. Sonder die Arabiese bydrae, sou die Renaissance waarskynlik nie plaasgevind het nie.
